🔎 Formulas

A downloadable Microsoft Word version of this formula sheet can be found at robmunger.com/2000share. Questions or comments? Please email rob.mgmte2000@gmail.com. Remember, your first reference is always the lectures and the homework.

Press Ctrl-D to bookmark this page. Feel free to download it, but please do not reupload.

L2 - Money and Banks

Bruce often refers to M1 as the “Money Stock” or the “Money Supply.”

$$\textbf{M1} = \text{Total Deposits} + \text{Cash Held by Public}$$ $$\textbf{M2} = M1 + \text{Time Deposits} + \text{Money Market Mutual Funds}$$

Definition of Bank Capital:

$$\textbf{Bank Capital} = \text{Assets} - \text{Liabilities}$$

With algebra, this implies that the left and right of balance sheet are equal: ️⚖️

$$\text{Assets} = \text{Liabilities} + \text{Bank Capital}$$

Bruce’s 6 Bank Balance Sheet Event Examples are helpful.

References: 2 Feb 4.ppt and L2-Bank Balance Sheets

L3 - Bank Profitability and Leverage

Name

Equation

Example

Net Interest Spread

= interest rate earned on assets - interest rate paid on liabilities

= 6% - 3% = 3%

Net Interest Income

Net Interest Income = (total interest received) - (total interest paid)

= $12M - $8M = $4M

Net Interest Margin

$= \frac{ \text{Net Interest Income} }{\text{Total Interest Earning Assets}}$

= $4M/$100M = 4%

Return on Assets (ROA)

$= \frac{\text{Profit After Taxes}}{\text{Total Assets}}$

= $1M / $100M = 1%

Return on Equity (ROE)

$= \frac{\text{Profit After Taxes}}{\text{Bank Capital}}$

= $1M / $10M = 10%

Leverage Ratio

$= \frac{\text{Assets}}{\text{Capital}}$

= $100M / $10M = 10 to 1

Debt To Equity Ratio

$= \frac{\text{Bank Liabilities}}{\text{Bank Capital}}$

= $90M / $10M = 9 to 1

Helpful Formula for Checking Work

ROE = ROA × Leverage Ratio

Checking the numbers:
10% = 1% × 10

Profit

= Δ Bank Capital

(Because profit increases your net worth)

L3 - Reserves

Name

Equation

Example

Required Reserves

= R × Checking Deposits

= 10% × $2B = $200M

Interpretation: The Fed decides how many dollars of reserves a bank is legally required to hold for every $100 of deposits.

TotalReserves

=Vault Cash + Deposits at Fed

= $50M + $250M = $300M

Interpretation: both Vault Cash and Deposits at the Fed count as reserves.
“Deposits at Fed” = "Deposits at the Central Bank"

ExcessReserves

= Total Reserves - Required Reserves

= $300M - $200M = $100M

Interpretation: Any reserves that are not required are excess reserves.

R + E

Total Reserves / Deposits

= $300M/$1B = 30% ⇨ If R + E = 30% and R=10%, then E must be 20%

Interpretation: R+E is the total percent of deposits kept as reserves.

L3 - Bonus Reserves Equations

Occasional questions may ask you to reason about excess and required reserves. With a tiny bit of algebra, these nine equations follow from what you’ve learned in class. I lay them out here systematically for reference. ($\text{\$RequiredRes}$ means “Dollars of Required Reserves,” etc.)

	Required Reserves Version	Excess Reserves Version	Required and Excess
To find: R or E	$R = \frac{\text{\$RequiredRes}}{\text{Deposits}}$	$E = \frac{\text{\$ExcessRes}}{\text{Deposits}}$	$R + E = \frac{\text{\$TotalRes}}{\text{Deposits}}$
To find: $Reserves	$\textbf{\$RequiredRes} = R × \text{Deposits}$	$\textbf{\$ExcessRes} = E × \text{Deposits}$	$\textbf{\$TotalRes} = (R+E) × \text{Deposits}$
To find: Deposits	$\textbf{Deposits} = \text{\$RequiredRes} × \frac{1}{R}$	$\textbf{Deposits} = \text{\$ExcessRes} × \frac{1}{E}$	$\textbf{Deposits} = \text{\$TotalRes} × \frac{1}{R+E}$

L3 - Money Multiplier

$$MS = M1 = \text{Total Deposits} + \text{Cash Held by Public}$$ $$\text{Money Multiplier: } \frac{1}{R+E} = \texttt{1/(R + E)}$$ $$\color{green}\Delta \text{Total Deposits} = \text{Initial Deposit} × \frac{1}{R + E}$$ $$\color{green}\Delta MS = \Delta \text{Deposits} + \Delta \text{Cash Held by Public}$$

References: 3 Feb 11.ppt and L3-Measures of Bank Profitability

L4/L5 - Monetary Policy

You can use the two green equations, above, for Deposits/Withdrawals and Open Market Operations. For an Open Market Operation, $\Delta CHP = 0$
References: 4 Feb 18.ppt and L4-Reserves

$i = r + \pi\;$ and $\;r = i-\pi$
($r$=real interest rate; $i$=nominal interest rate; $π$=inflation rate)
References: 5 Feb 25.ppt and L5-Outline

L6 - NPV and IRR

$$\textbf{FV} = PV × (1 + i)^N$$ $$\textbf{PV} = \frac{FV}{(1 + i)^N}$$

Present Value of a stream of payments for T years:

$$\text{PV} = \frac{Pmt_1}{(1 + i)^1} + \frac{Pmt_2}{(1 + i)^2} + \frac{Pmt_3}{(1 + i)^3} + \cdots + \frac{Pmt_T}{(1 + i)^T}$$

To enter the above formula as plain text, write: PV = PMT1/(1+i)^1 + PMT2/(1+i)^2 PMT3/(1+i)^3 + ... + PMTT/(1+i)^T

$\text{PV of a Perpetuity} = \frac{\text{Yearly Pmt}}{i}$

$\text{NPV} = \text{PV of Cash Inflows} - \text{PV of Cash Outflows}$

To solve an IRR problem, write down NPV=0 or PVInflows = PVOutflows and solve for i.

NPV Rule: Undertake any project with a positive NPV. If two mutually exclusive projects have positive NPV, undertake the project with the higher NPV. (NPV is like the profit of the project.)

IRR Rule: Undertake any project for which the IRR is greater than the opportunity cost of capital.

References: 6 Mar 4.ppt and L6-Outline

Midterm

L7 - Bonds

F=Face value; T=Number of years until bond expires; i=discount rate/Interest rate; c=Coupon rate; Fc=F×c=a single coupon payment

$P_{ZCB}$ $= \frac{F}{(1 + i)^T}$

$P_{Consol}$ $= \frac{Fc}{i}$

$P_{CouponBond}$ $= \frac{Fc}{(1 + i)^1} + \frac{Fc}{(1 + i)^2} + \frac{Fc}{(1 + i)^3} + \cdots + \frac{Fc}{(1 + i)^T} + \frac{F}{(1 + i)^T}$

For a 3 year coupon bond:

$$P_{CouponBond} = \frac{Fc}{(1+i)^1} + \frac{Fc}{(1+i)^2} + \frac{Fc+F}{(1+i)^3}$$

Plain Text Formulas:

• 2 Year Coupon Bond: PB = Fc/(1+i)^1 + (Fc+F)/(1+i)^2
• 3 Year Coupon Bond: PB = Fc/(1+i)^1 + Fc/(1+i)^2 + (Fc+F)/(1+i)^3
• T Year Coupon Bond: PB = Fc/(1+i)^1 + Fc/(1+i)^2 + Fc/(1+i)^3 + ... + (Fc+F)/(1+i)^T
• Zero Coupon Bond: PB = F/(1+i)^T

Shortcut to calculate price of a 4 year coupon bond with F=$1000, i=8$60)

• PB = 60/1.08 + 60/1.08^2 + 60/1.08^3 + 1060/1.08^4
  
  

Equivalent Tax Free Rate: $\text{Taxable Rate} × (1 - \text{Marginal Tax Rate})$

To solve a Yield To Maturity (YTM) problem, write down the bond pricing formula and solve for i.

References: 7 Mar 25.ppt, L7-Outline, and L7-Notes

L8/L9 - Stocks & Investment Companies

Authorized Shares = Issued Shares + Unissued Shares
Issued Shares = Shares Outstanding + Treasury Stock
Shares Outstanding = Float + Restricted Shares
My “Classes of Shares” worksheet can you help solve problems using the above equations.
Market Capitalization: Market “Cap” = Shares Outstanding × Price Per Share

$$\text{Net Asset Value (NAV)} = \frac{\text{Market Value of Assets} - \text{Liabilities}}{\text{Shares Outstanding}}$$
$$R = \frac{NAV_1 - NAV_0 + \text{Income} + \text{Capital Gain}}{NAV_0}$$

References: 8 Apr 1.ppt, L8-Outline, L8 Notes, 9 Apr 8.ppt, and L9 Notes

L10 - CAPM and EMH

CAPM: $E(r_S) = r_F + β[E(r_M) - r_F]$

CAPM Jargon:

$E(r_S)$ $= E(r_i) =$ Expected return on a portfolio or individual stock
$E(r_M)$ = Expected return on the market portfolio
$r_F$ = risk free rate = rate on return of assets considered to be risk-free = return on T-Bills
“Risk Premium” means you subtract off the risk free rate.
$E(r_M) - r_F$ = Market risk premium = Expected risk premium of market

Expected Value (EV):

= Probability of Outcome 1 × Value of Outcome 1
+ Probability of Outcome 2 × Value of Outcome 2
+ Probability of Outcome 3 × Value of Outcome 3
+ …
+ Probability of Outcome N × Value of Outcome N

EMH stock price = PDV of EV of future price + PDV of dividend

Example: $EV_{Price} = \frac{1}{3}(\$12) + \frac{1}{3}(\$18) + \frac{1}{3}(\$24) = \$18$
Stock price = $PDV \text{ of } EV + PDV \text{of Dividend}$
Stock price = $\frac{\$18}{(1+12\%)} + \frac{\$3}{(1+12\%)}$

References: 10 Apr 15.ppt and L10 Notes

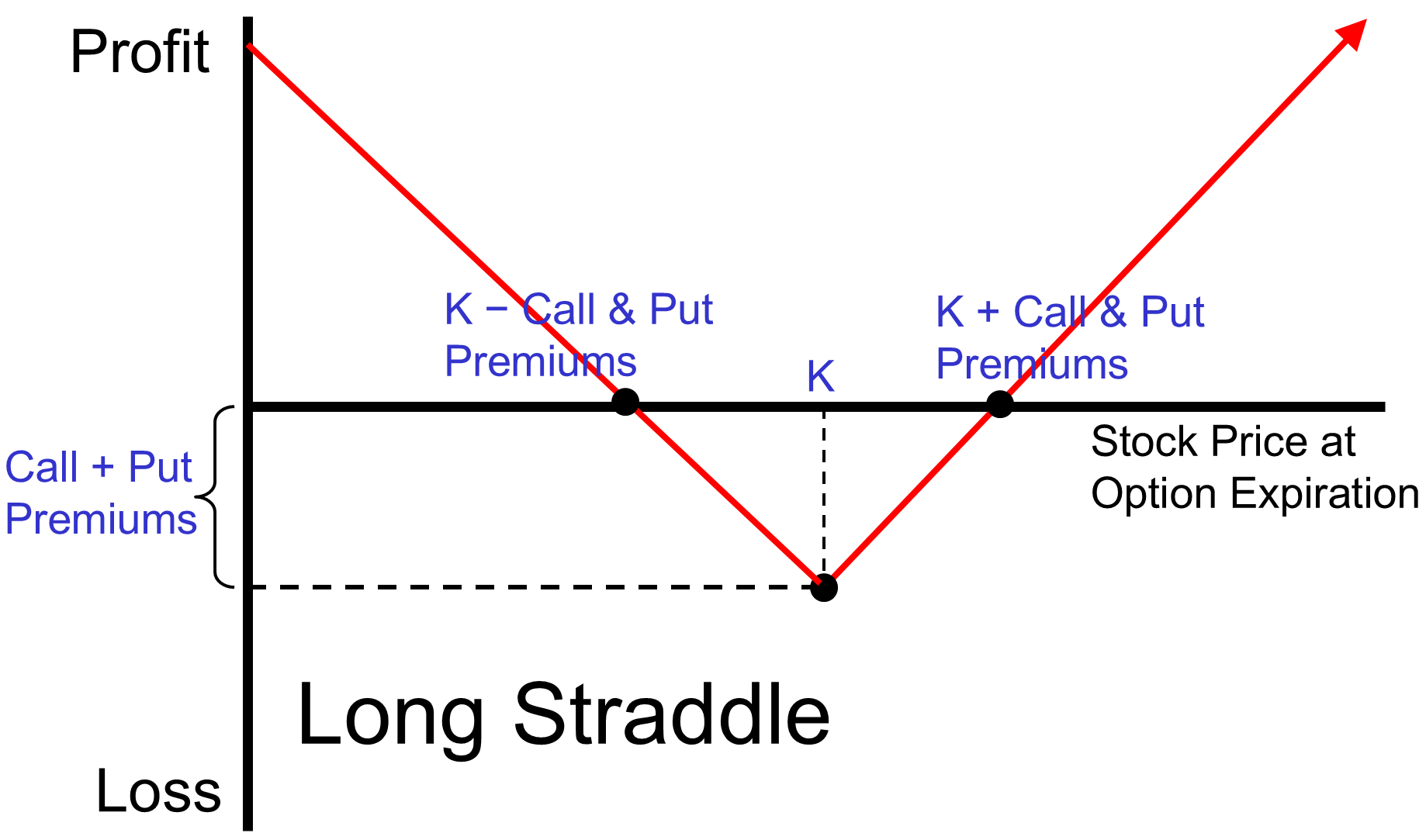
L11 Options

Call IV $= \text{Max} (S-K, 0)$
Put IV $= \text{Max} (K-S, 0)$

P/L from Buying an Option $= IV - Pr$

P/L from Buying a Call $= \text{Max} (S-K,0) - Pr$
P/L from Buying a Put $= \text{Max} (K-S, 0) - Pr$

P/L from Selling an Option $= Pr - IV$

P/L from Selling a Call $= Pr - \text{Max} (S-K, 0)$
P/L from Selling a Put $= Pr - \text{Max} (K-S, 0)$

Premium = Intrinsic Value + Time Value

Premium = EV of the gain from an option or strategy

Leverage = Share Price×100 / Premium×100

	Buy/Long	Write/Sell/Short
Call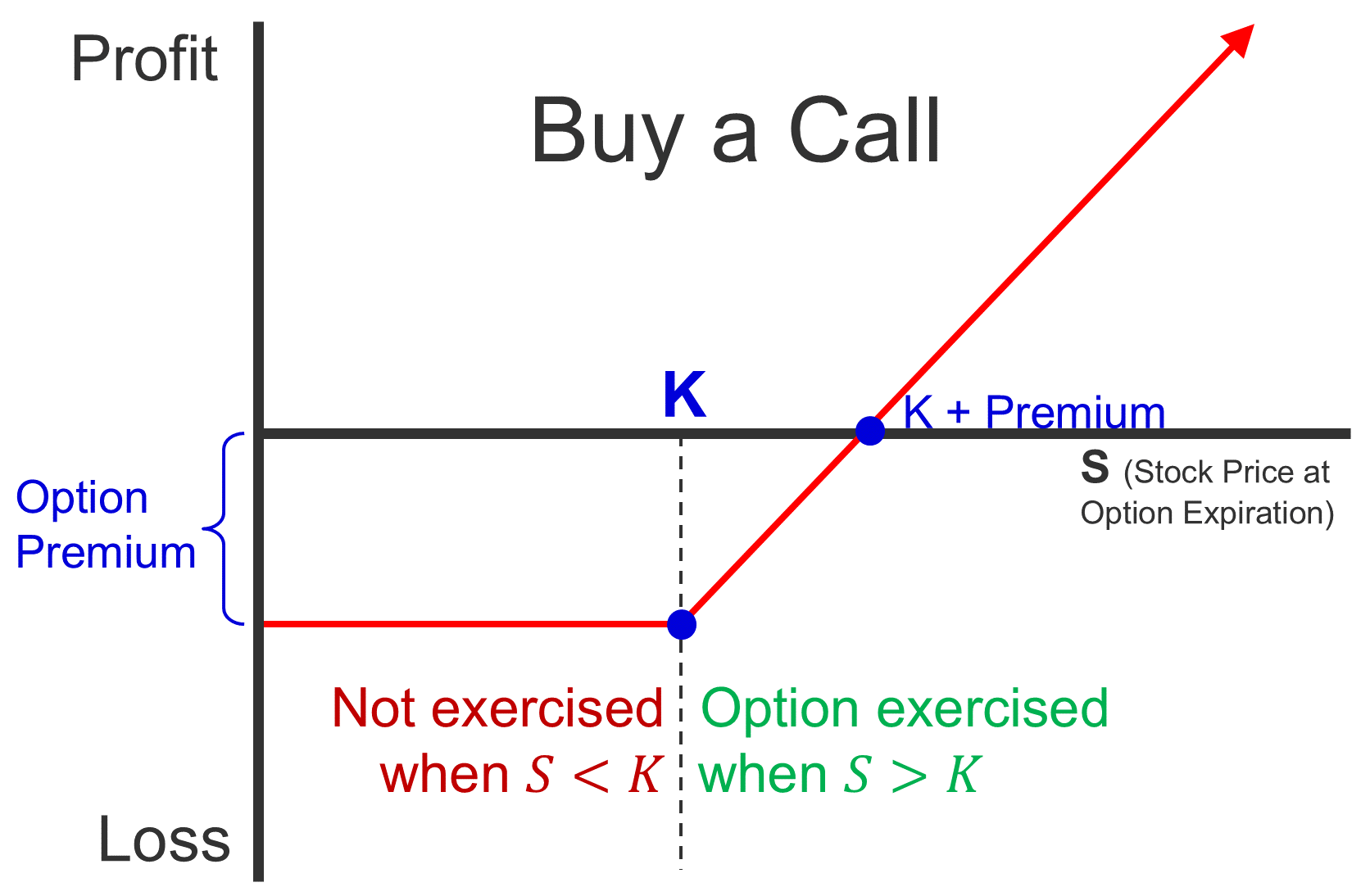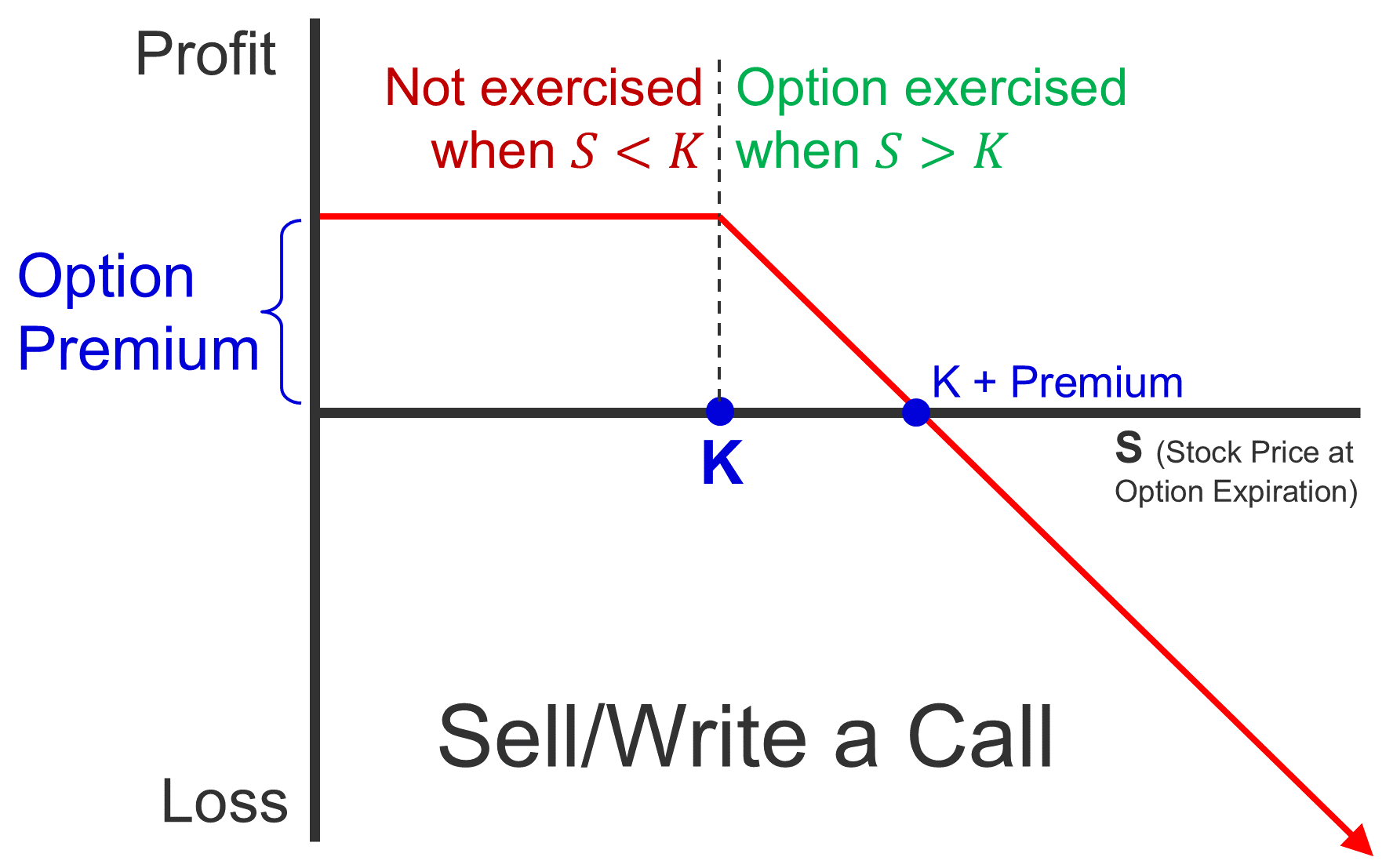
Put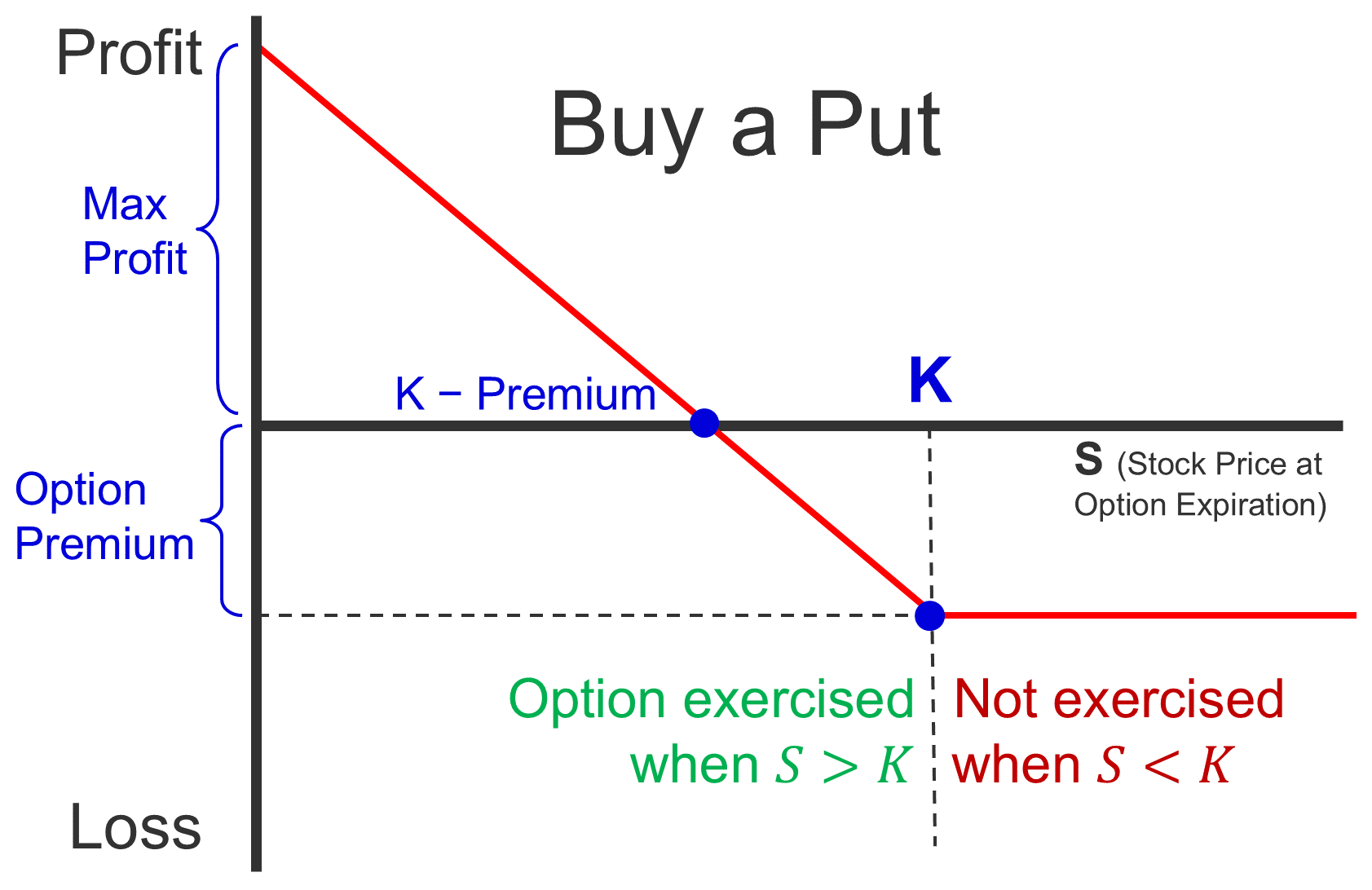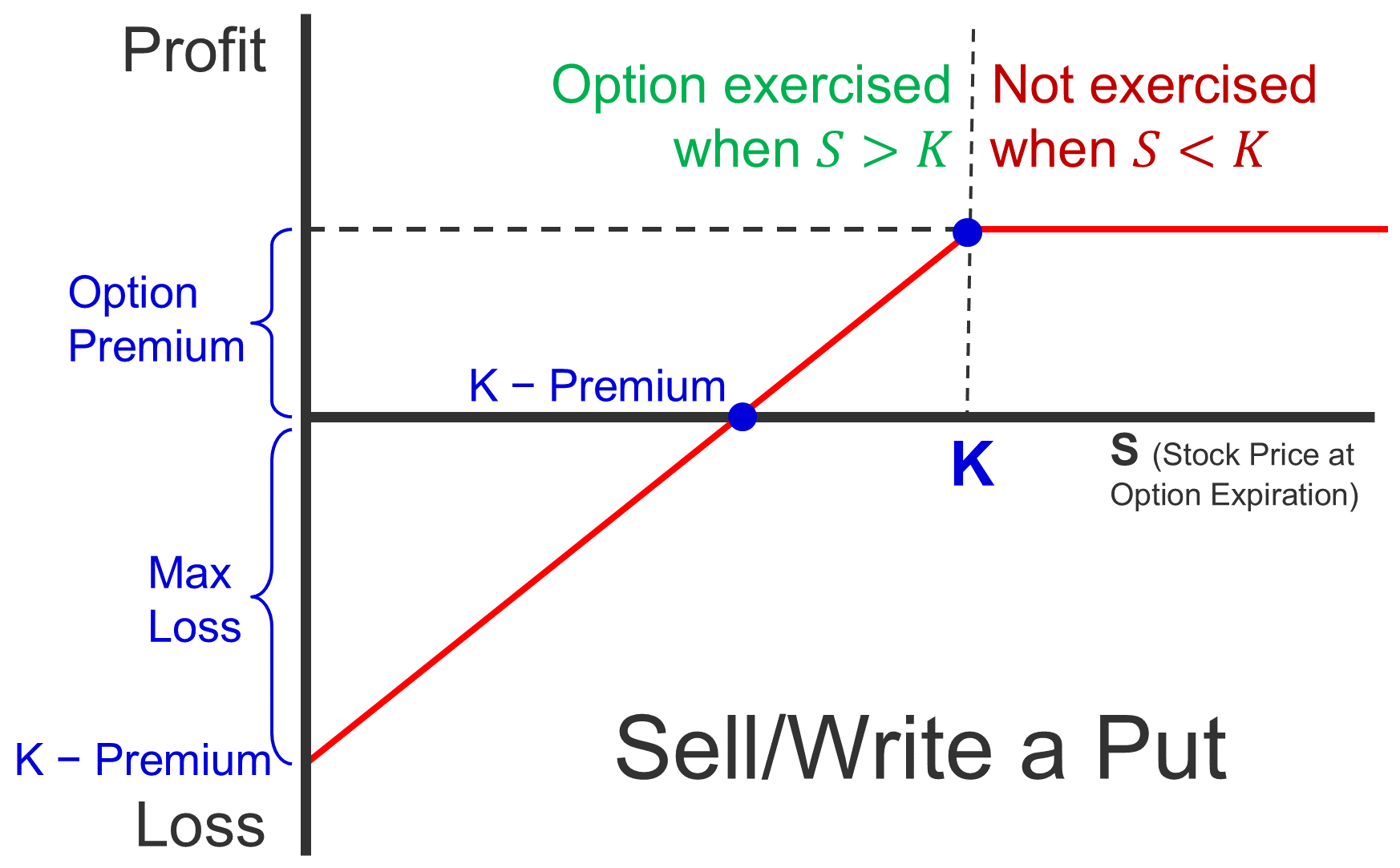

References: 11 Apr 22.ppt and L11 Notes

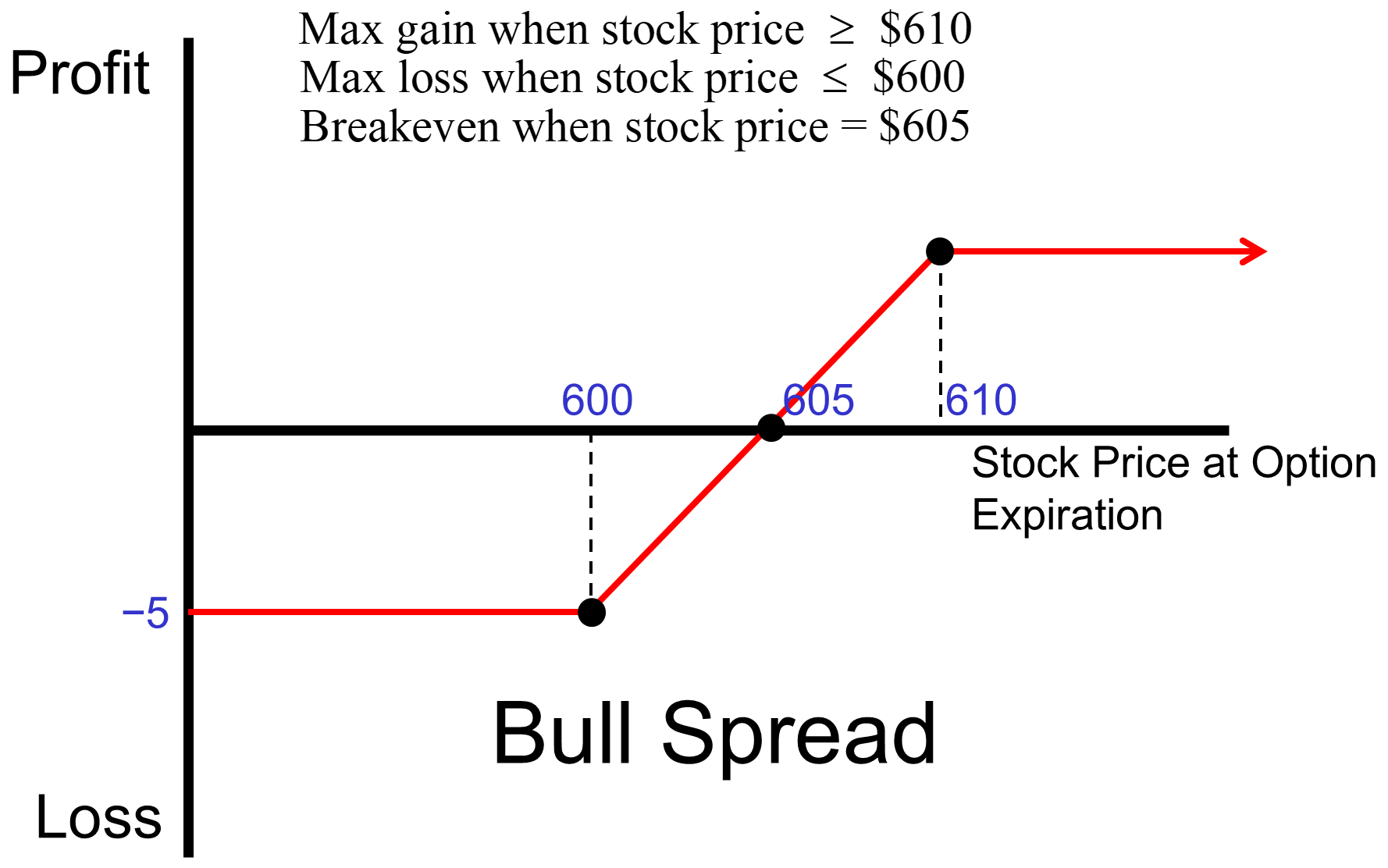
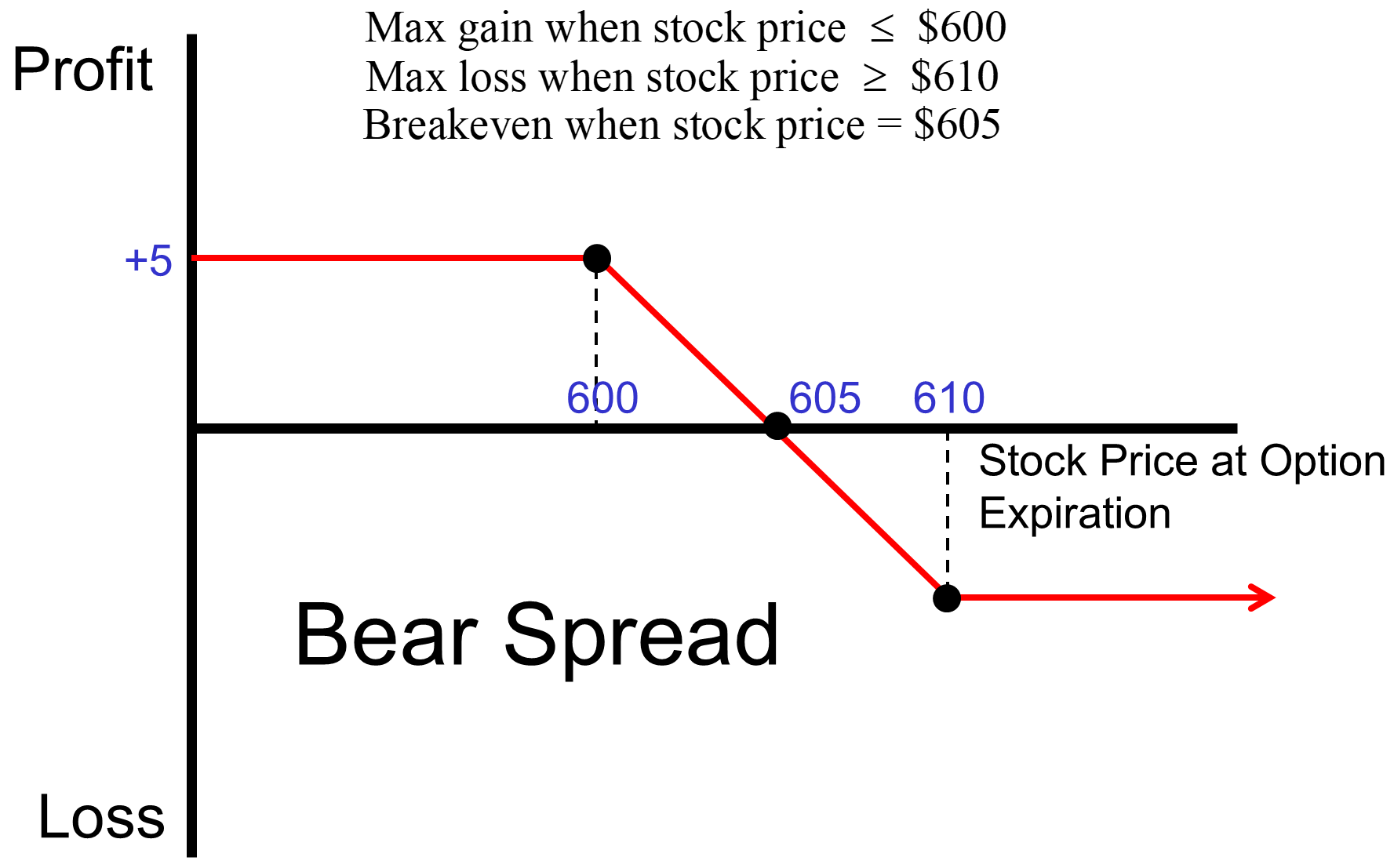
L12 Options Strategies

Spreads	Straddles

References: 12 Apr 29.ppt, and L12 Notes

Futures

$\Delta\text{Price} = (\text{NewPrice} - \text{OldPrice})$
Buy the contract: $P/L = ∆\text{Price} × \text{ContractSize}$
Sell the contract: $P/L = -∆\text{Price} × \text{ContractSize}$
$\text{ContractSize = 5000 bushels wheat}$ (for example)
$\text{ContractSize = \$50 per point of S\&P 500}$ ($250 for ‘full-sized contract,’ $50 for e-mini, and $5 for micro e-mini)
$\text{Value of contract} = \text{ContractPrice} × \text{ContractSize}$ $\text{Leverage} = \frac{\text{Value of Contract}}{\text{Initial Margin}}$

References: 13 May 6.ppt, L13 Notes

© 2025 Rob Munger