🔎 IRR problems that can't be solved with Algebra

These techniques can be helpful if you have an IRR question that you can’t solve algebraically. (You can also use these techniques for Yield problems with Bonds)

As described on the following slide, the IRR is the value of i that makes:

$\text{PV of Cash Inflows} = \text{PV of Cash Outflows}$
  i.e. that makes: $NPV = 0$

Therefore, there are two required steps for any IRR problem:

1. Find a value if i that makes those two equations true. (If it makes one equation true, it makes both of them true because the two equations mean the same thing.)
2. Demonstrate that the value of i makes one of the equations true.

Elsewhere, I have said that I like using the first equation because it saves a couple steps of algebra. Therefore, on this page, I’ll be looking for a value of i that makes the PV of Inflows equal to the PV of Outflows.

While I do provide example solutions on this page, please note that Bruce expects you to put your solutions into your own words. Please use these examples as a way to understand the techniques and then write the ideas out without referring to these examples. Definitely don’t copy and paste them in.

Guess and Check

✏️ Suppose you have a business opportunity with the following cash flows:

T	Cash Outflows	Cash Inflows	Net Cash Flows
0	$100K		-$100K
1		$400K	$400K
2		$400K	$400K
3		$200K	$200K
4		$900K	$900K

What is the IRR of this opportunity?

We need to find a value of i that makes $\text{PV (Inflows)} = \text{PV (Outflows)}$.
(I’ll do everything in thousands of dollars…)
$\text{PV (Inflows)} = \frac{400}{(1+i)^1} + \frac{400}{(1+i)^2} + \frac{200}{(1+i)^3} + \frac{900}{(1+i)^4}$
$\textcolor{black}{\colorbox{f8f398}{\text{PV (Outflows)} = 1000}}$
Our goal is to find some value of i, where $\text{PV (Inflows)}$ equals 1000. The first technique we will try is a brute force approach called “Guess and Check.” It takes a while, but it’s easy to understand.

Suppose $i = \textcolor{black}{\colorbox{bd7be1}{1\%}}$, then:

$$\text{PV (Inflows)} = \frac{400}{(1+i)}^1 + \frac{400}{(1+i)^2} + \frac{200}{(1+i)^3} + \frac{900}{(1+i)^4}$$ $$= \frac{400}{(1+1\%)^1} + \frac{400}{(1+1\%)^1} + \frac{200}{(1+1\%)^1} + \frac{900}{(1+1\%)^1} = \textcolor{black}{\colorbox{bd7be1}{1,847}}$$

Suppose $i = \textcolor{black}{\colorbox{8791e7}{2\%}}$, then:

$$\text{PV (Inflows)} = \frac{400}{(1+2\%)^1} + \frac{400}{(1+2\%)^2} + \frac{200}{(1+2\%)^3} + \frac{900}{(1+2\%)^4} = \textcolor{black}{\colorbox{8791e7}{1,796}}$$

Suppose $i = \textcolor{black}{\colorbox{8ae787}{5\%}}$, then:

$$\text{PV (Inflows)} = \frac{400}{(1+5\%)^1} + \frac{400}{(1+5\%)^2} + \frac{200}{(1+5\%)^3} + \frac{900}{(1+5\%)^4}=\textcolor{black}{\colorbox{8ae787}{1,656}}$$

Suppose $i = \textcolor{black}{\colorbox{e78787}{20\%}}$, then:

$$\text{PV (Inflows)} = \frac{400}{(1+20\%)^1} + \frac{400}{(1+20\%)^2} + \frac{200}{(1+20\%)^3} + \frac{900}{(1+20\%)^4} = \textcolor{black}{\colorbox{e78787}{1,160}}$$

Suppose $i = \textcolor{black}{\colorbox{e0b063}{28\%}}$, then:

$$\text{PV (Inflows)} = \frac{400}{(1+ 28\%)^1} + \frac{400}{(1+ 28\%)^2} + \frac{200}{(1+ 28\%)^3} + \frac{900}{(1+ 28\%)}^4 = \textcolor{black}{\colorbox{e0b063}{987.28}}$$

Suppose $i = \textcolor{black}{\colorbox{7be1be}{27.334\%}}$, then:

$$\text{PV (Inflows)} = \frac{400}{(1+ 27.334\%)^1} + \frac{400}{(1+ 27.334\%)^2} + \frac{200}{(1+ 27.334\%)^3} + \frac{900}{(1+ 27.334\%)^4} = \textcolor{black}{\colorbox{7be1be}{1,000.0531}}$$

[Note, you don’t have to include as many steps as I did. Just put down your last couple of steps so the grader can see that you get the point.]

Because the $\text{PV(Inflows)} = \text{PV(Outflows)}$ when $i = 27.334\%$, the IRR is $27.334\%$.

Using a spreadsheet to “Guess and Check”

You can speed up the “Guess and Check” method by using a spreadsheet to try numbers out more quickly:

🔎 Guess and Check method - Spreadsheet1

Using a financial calculator or spreadsheet financial function

While you are welcome to use a financial calculator or a spreadsheet function to find the IRR, you will still need to demonstrate that your value of i makes one of the two equations true. You also need to demonstrate that you know that this makes your value of i the IRR.

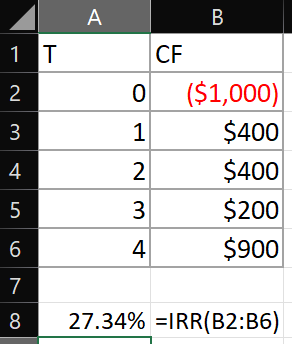
In most spreadsheets, the built-in function used to calculate IRR is, not surprisingly, $=IRR()$. Here is an example of a Google Sheet spreadsheet that I use to solve the problem on this page: Solving IRR questions in Google Sheets (free)

Google Sheets is a free program available to anyone with a Gmail account. It is just as powerful as Excel, but it is better for situations where you need to work on a document simultaneously with different people. (If you have Excel, it’s a bit easier to use, though, because it doesn’t run in a web browser.) If you have a Gmail account, just go to sheets.google.com to start using Google Sheets.

✏️ Re-solve the above problem using a spreadsheet built in functions.

✔ Click here to view answer

The IRR is a value of i that makes $\text{PV (Inflows)} = \text{PV (Outflows)}$.

(I’ll do everything in thousands of dollars…)

$\text{PV (Inflows)} = \frac{400}{(1+i)^1} + \frac{400}{(1+i)^2} + \frac{200}{(1+i)^3} + \frac{900}{(1+i)^4}$
$\text{PV (Outflows)} = 1000$

Our goal is to find some value of i, where $\text{PV (Inflows)}$ equals 1000, which is the PV of the outflows. I used a spreadsheet to find the value of i that accomplishes this. $i = 27.3367\%$

When $i = 27.3367\%$, then:

$\text{PV (Inflows)} = \frac{400}{(1+27.3367\%)^1} + \frac{400}{(1+27.3367\%)^2} + \frac{200}{(1+27.3367\%)^3} + \frac{900}{(1+27.3367\%)^4} = 1,000.0008$

Because the $\text{PV of the Inflows} = \text{PV of the Outflows}$ when $i = 27.3367\%$, the $IRR$ is $27.3367\%$.

The following can be used to find that $i=27.34\%$ solves $\text{PV (Inflows)}= \text{PV (Outflows)}$, but it is not sufficient to get credit. To get credit, you have to write up something like the above ↑: