👨‍🏫 Outline

Formulas for this lecture can be found in my paper formula sheets and online formula sheet.

Future Value and Present Value

Future values tells you how much you will have in N years, if you invest PV today at an interest rate i:

$$FV=PV(1+i)^N$$

Present value tells you how much you need to invest today, to get a certain amount of cash flow in the future, assuming that you can invest your money at an interest rate, i.

$$PV=\frac{FV}{(1+i)^N}$$

PV also tells you the “fair value” of any investment because it tells you how much you would need to invest to recreate the investment. This “fair value” is the most you should pay for the investment today. To calculate it, just calculate the PV of all of the cash flows from the investment.

The discount rate, i

Most often, when Bruce wants to tell you what you should use as your discount rate (ie $i$) in a problem, he tells you how much you would earn on the money if you invested it in something else. He might also tell you the return that similar investments are earning. This known as the opportunity cost of capital.

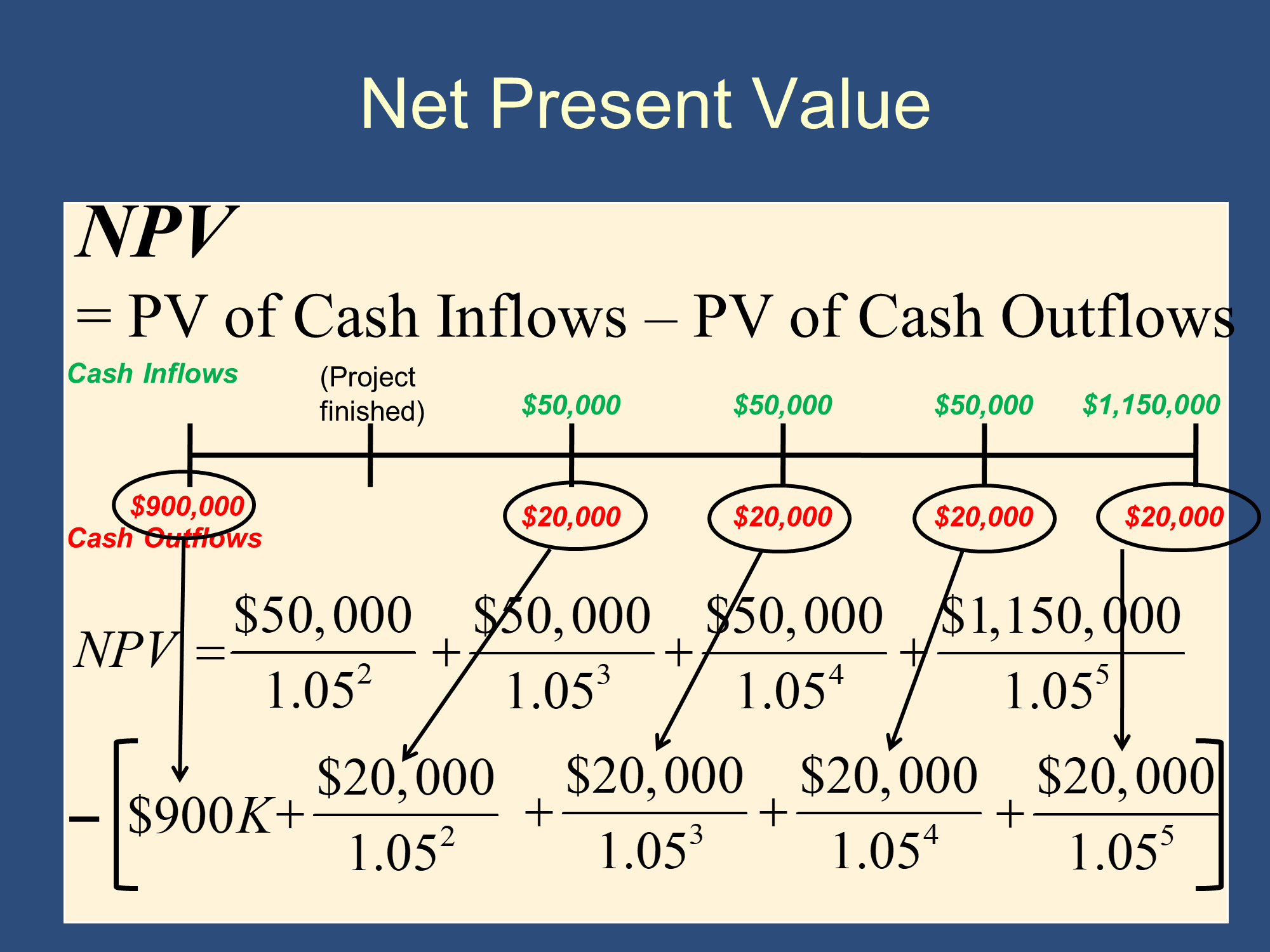
Net Present Value (NPV)

$$NPV = \text{PV of Cash Inflows} - \text{PV of Cash Outflows}$$

NPV tells you how profitable a project is, when you take time into account.

Internal Rate of Return (IRR)

Internal Rate of Return is the value of i that makes

$$\text{PV of Cash Inflows} = \text{PV of Cash Outflows}$$

i.e. it is the value of i that makes

$$NPV = 0$$

Intuitively, the IRR tells you the ”%-return” on a project or investment. It tells you the profitability as a percentage.

NPV Rule, IRR Rule

NPV Rule:

1. Undertake any project with a positive NPV
2. In case two mutually exclusive projects have positive NPV, undertake the project with the higher NPV

IRR Rule: Undertake any project for which the IRR is greater than the opportunity cost of capital

Perpetuities

Perpetuity formula: If you will be receiving a cash flow of CF every year (forever), then the PV of that cash flow is $PV = \frac{CF}{i}$

Examples

NPV Example

✏️ Your private equity firm is considering buying out a corporation. You expect to purchase it for $100M today. Then you will invest $40M into it this next year (payable at the end of this coming year). You will also invest $20M into it the following year (payable at the end of the second year). Finally, you will sell it for $280M at the end of the second year. What is the NPV of this purchase. Given that this is a risky project, your cost of capital is 14%. Should you invest?

✔ Click here to view answer

Time	Cash Inflow (M)	Cash Outflow (M)
0		100
1		40
2	280	20

$i=14\%$
(If he gives you a random percent number in an NPV, IRR or bond problem, it is likely to be the discount rate. Synonyms include “cost of capital” “similar investments have a return/yield of” “discount rate” “opportunity cost of capital.“)

$$\text{PV Inflows} = \frac{\$280}{(1+14\%)^2} = \$215.45$$$$\text{PV Outflows} = \frac{\$100}{(1+14\%)^0} + \frac{\$40}{(1+14\%)^1} + \frac{\$20}{(1+14\%)^2} = \$150.48$$$$NPV = \$215.45 - \$150.48 = \$64.97$$

Combining everything into one shortcut and remembering that $1+14\%=1.14$

$$NPV = \frac{\$280}{1.14^2} - \$100 - \frac{\$40}{1.14} - \frac{\$20}{1.14^2} = \$64.97$$

We should invest, because $NPV>\$0$

To calculate any IRR, you always follow the three steps:

1. write down the PV of the cash inflows (leave the discount rate as i)
2. write down the PV of the cash outflows (leave the discount rate as i)
3. set the two formulas equal, and solve for i.

See below for an example of how to do this.

IRR example (1 period)

✏️ Your private equity firm is considering buying out a corporation. You expect to purchase it for $100M today. Then you will invest $80M into it, payable immediately. You will sell it for $280M at the end of the first year. What is the IRR of this purchase? If your cost of capital is 14%, should you invest?

✔ Click here to view answer

Start with a timeline:

Time	Cash Inflow (M)	Cash Outflow (M)
0		100+80
1	280
2

Our instructions for solving an IRR question are as follows: To calculate any IRR, you always follow the three steps:

1. write down the PV of the cash inflows (in terms of a variable, i)
     $\text{PV of Inflows} = \frac{280}{(1+i)^1}$
2. write down the PV of the cash outflows
     $\text{PV of Outflows} = 180$ (we don’t need to discount it because we pay immediately)
3. set the two formulas equal, and solve for i.

$$\frac{280}{(1+i)^1} = 180$$

You can ignore an exponent of 1:

$$\frac{280}{(1+i)} = 180$$

I call this step the “switcheroo:”

$$\frac{280}{180} = (1+i)$$$$\frac{280}{180} = 1.5556 = 1+i$$

Recopying:

$$1.5556 = 1+i$$

Subtract 1 from both sides:

$$i = .5556 = 55.56\%$$

The IRR is 55.56%. Because this is higher than your cost of capital (14%), you should invest.

You could also decide whether to invest using the NPV rule. However, since we’ve already calculated the IRR, it is easier to use the IRR rule.

IRR example (perpetuity)

✏️ You are starting a side hustle, that will earn $10,000 per year, every year, forever. It will cost you $80,000 to set up. You only pay the $80,000 once (immediately). Suppose that you would borrow $80,000 with a cost of capital of 18.2%. Calculate the IRR and use the IRR to determine whether you should invest.

✔ Click here to view answer

We recall the Perpetuity formula: $PV = \frac{CF}{i}$

$$\text{PV of cash inflows} = \frac{\$10,000}{i}$$$$\text{PV of cash outflows} = \$80,000$$$$\begin{aligned} \frac{\$10,000}{i} &= \$80,000 \\ \frac{\$10,000}{\$80,000} &= i \\ \end{aligned}$$

Calculator: $\frac{10,000}{80,000}=0.125$
$i = .125 = 12.5\%$
In this case, our cost of capital is 18.2%. We will pay 18.2% to borrow the money, but we only have a profit of 12.5%, so it won’t be profitable enough. The IRR rule says to reject the project.

IRR Example (single payment)

Let’s revisit the private equity example. Suppose that instead of receiving the $280M in one year, you receive it in two years…

✏️ Your private equity firm is considering buying out a corporation. You expect to purchase it for $100M today. Then you will invest $80M into it, payable immediately. You will sell it for $280M at the end of the second year. What is the IRR of this purchase? If your cost of capital is 14%, should you invest?

Time	Cash Inflow (M)	Cash Outflow (M)
0		100+80
1
2	280

✔ Click here to view answer

Remember that to calculate any IRR, you always follow the three steps:

1. write down the PV of the cash inflows
2. write down the PV of the cash outflows
3. set the two formulas equal, and solve for i.

$$\text{PV Inflows} = \frac{280}{(1+i)^2}$$$$\text{PV Outflows} = 180$$

For IRR, solve

$$\text{PV Inflows} =\text {PV Outflows}$$

(this is often easier than solving $NPV=0$)

$$\frac{280}{(1+i)^2} = 180$$

Switcheroo:

$$(1+i)^2 = \frac{280}{180} = 1.56$$$$(1+i)^2 = 1.56$$$$1+i = 1.56^\frac{1}{2}$$

↑ Algebra: you take the ($\frac{1}{2}$) exponent of both sides.

$$1 + i = 1.249$$$$i = .249 = 24.9\%$$

Your IRR of 24.9% is still higher than your cost of capital. Therefore, you should still invest.