🔎 PDV and IRR (With Examples)

NPV is important because one of the key drivers of whether to buy or sell any investment is whether it is underpriced or overpriced. NPV tells you what the fair price of a security is, so you can compare the market price to the fair price and “buy the securities that are ‘on sale’ while selling the securities that are overpriced.”

IRR is vitally important because it underlies all concepts of “percent return,” such as Holding Period Return.

PDV

Imagine that you are evaluating a new business opportunity. With the new opportunity, you will receive $1.3 million in one year. If you don’t take that opportunity, you will invest in a “default investment” that will earn 10%. What is the fair price of this investment opportunity?

To answer this we ask: How much you would need to invest in your “default investment” to get the $1.3M that this new opportunity will give you?

Plug and chug: (help)

1. Equation → $FV = \text{Initial Investment} \times (1+i)^1$ (for example $FV = \$100 \times (1+10\%)^1=\$110$)
   FV that I want = $\$1.3M$
   $\text{Present Value} = \text{Initial investment}$
   How much does that initial investment need to be so that if I invest it in my default investment I earn the $1.3M I would get from the new investment I’m analyzing.
2. Plug 🔌 → $\$1.3M = \text{Initial Investment} \times (1+10\%)^1$
3. Chug 🚂 → $\frac{\$1.3}{1+10\%^1}=\$1.18M$

If I invest $1.18M in my default investment today (in the present), I will end up with $1.3M next year.

What this means is that by investing $1.18M in your default investment, you can get exactly the same cash flows as new opportunity.

This new investment should be worth exactly $1.18M to you. The algebra we used gave us the following formula:

$\text{Fair value} = \frac{\$1.3M}{1+10\%^10} = \frac{CF}{(1+i)^T}$

We call the amount you would have to invest in your “default investment” the “Present Discounted Value” (“PDV”) of any business opportunity.

$$PDV = \frac{CF}{(1+i)^1}$$

If most of the market can also earn 10% elsewhere, market participants will consider $1.18M to be the fair value of the opportunity. Market participants can use this calculation to find a fair price to facilitate deals. They can also use the calculation to evaluate whether the price they are offered is a good price or a bad price.

WE CAN USE THIS PRINCIPLE TO FIND THE FAIR VALUE OF BONDS, STOCKS, AND OPTIONS. And we will.

We can also calculate how much we would need to invest in our “default investment” to get more complex cash flows. We can show, using algebra like the above, that if we have an investment that would provide cash flows CF1, CF2, CF3, CF4, … , and CFT at times 1, 2, 3, 4, … and T years from now, that we would need to invest:

$PDV = \frac{CF_1}{(1+10\%)^1} + \frac{CF_2}{(1+10\%)^2} + \frac{CF_3}{(1+10\%)^3} + \frac{CF_4}{(1+10\%)^4} + ... \frac{CF_T}{(1+10\%)^T}$

PDV and Bonds

✏️ Suppose you had a contract that paid you the following cash flows:

Time	Payments
0	0
1	0
2	0
3	0
4	0
5	F=Face Value=1000

Suppose that if you didn’t buy this contract, you would invest your money and earn a 10% return. What would the fair price of this contract?

✔ Click here to view answer

This contract is called a zero coupon bond.

$P_{ZCB} = \frac{\$1000}{(1+10\%)^S} = \frac{F}{(1+i)^T} = \frac{\$1000}{1.1^5} = \$620.92$

The fair value is $\$620.92$.

✏️ Suppose you had a contract that paid you the following cash flows:

Time	Payments
0	$0
1	$\$23=2.3\% \times \$1000=c \times F$ c = coupon rate F = Face Value	$\frac{\$23}{(1+10\%)^1}$
2	$\$23$	$\frac{\$23}{(1+10\%)^2}$
3	$\$23$	$\frac{\$23}{(1+10\%)^3}$
4	$\$23$	$\frac{\$23}{(1+10\%)^4}$
5	$\$23 + 1000$	$\frac{\$23}{(1+10\%)^5} + \frac{\$1000}{(1+10\%)^5}$

As before, assume that $i=10\%$. What would the fair price of this contract?

✔ Click here to view answer

$PDV = \frac{CF_1}{(1+10\%)^1} + \frac{CF_2}{(1+10\%)^1} + \frac{CF_3}{(1+10\%)^3} + \frac{CF_4}{(1+10\%)^4} + ... \frac{CF_T}{(1+10\%)^T}$

$PDV = \frac{\$23}{(1+10\%)^1} + \frac{\$23}{(1+10\%)^2} + \frac{\$23}{(1+10\%)^3} + \frac{\$23}{(1+10\%)^4} + \frac{\$23}{(1+10\%)^5} + \frac{\$1000}{(1+10\%)^5} = \$708.11$

The fair value of this bond is $\$708.11$. It is worth $\$708.11$ to you.

✏️ Imagine you are evaluating a zero coupon bond. With the zero coupon bond, you will receive $1.3 million in five years. What is the fair price of this bond? If you don’t buy this bond, you will invest in a “default investment” that will earn 10%.

✔ Click here to view answer

To answer this we ask: How much you would need to invest in your “default investment” to get the $1.3M that this zero coupon bond will give you?

Plug and chug: (help)

1. Equation → $PB \times (1+10\%)^5 = \$1.3M$
2. Plug 🔌 →
3. Solve 🚂 → $PB = \$1.3M \times (1+10\%)^5 = \frac{1.3}{(1.1)^5} = \$0.807M$
4. 🧠 →

✏️ Suppose a bond will pay you $23 starting next year, every year, forever. How much should that bond cost? Suppose other bonds pay an interest rate of 10%.

✔ Click here to view answer

$P_C = \frac{\$23}{10\%} = \$230$

This type of bond is called a Consol.

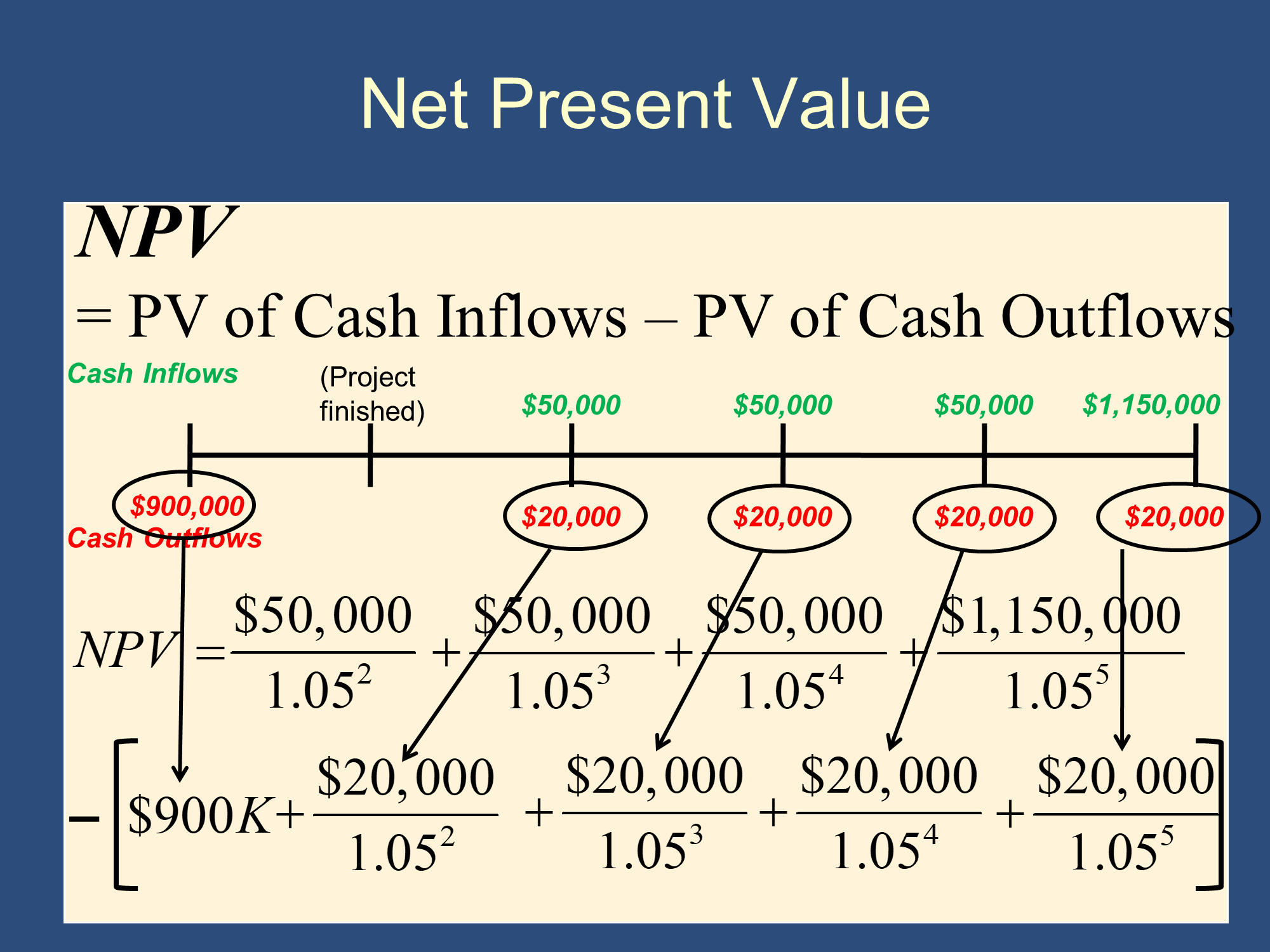
NPV

We can also evaluate opportunities where we get cash inflows at different times:

We can also evaluate opportunities with cash inflows and outflows by subtracting the outflows from the inflows:
$NPV = \text{PDV(Inflows)} - \text{PDV(Outflows)}$
(PDV and PV are more or less the same. It’s a bit more complex than that, but don’t worry.)

IRR

What we saw above is that by solving the future value formula for the initial investment, we get the formula for PDV.

If we solve the NPV formula for i, we get the IRR, which tells us the (Internal) Rate of Return of our investment.

Takeaway: for any IRR problem, solve it by writing down a formula and then solving for i. (For some problems, there is another way. See below).

IRR tells you the effective annual return of the project, as a percentage.

The idea of IRR is that there is a specific interest rate which makes the PV(Inflows) = PV(Outflows) of the project. In other words, you put money into the project at various different times (Inflows). You also take money out of the project at various times (outflows). What interest rate would make those two equal? That’s the interest rate you are earning on the project (IRR).

🙋‍♀️You aren’t making any excess profit when PV(Inflows) = PV(Outflows), but you ARE earning a return of i (IRR) on your investment.

🙋‍♀️IRR is just like looking at the interest rate on a deposit account at your bank. Suppose $i=.5\%$. We may have a target rate for how much we hope to earn when we invest our money in a deposit account. Suppose that target rate (or hurdle rate) is $.6\%$. In this case, we would decide that this bank isn’t good enough and we would look for another one. This is related to the IRR rule:

Whenever you see an IRR problem, you will ALWAYS write down the following formula and then substitute numbers into it: $\text{PV(Inflows)} = \text{PV(Outflows)}$.

Two other ways to think of it:

1. Cost of capital
2. Return on other similar investments. ←Teo

Example IRR problems

How to solve:

for any IRR problem, solve it by writing down a formula [PV(Outflows) = PV(Inflows)] and then solving for i

Note: some people will write down NPV=0 for their formula rather than PV(Inflows)=PV(Outflows), but this tends to add a step to the algebra AND it will make it a bit harder when we learn bonds if you use that version.

✏️ Suppose I lend $358 today and am paid back $487 in 1 year. What is the effective interest rate on the loan?

✔ Click here to view answer

Write down formula from my perspective:
$\text{PV(Outflows)} = \$358$

$\text{PV(Inflows)} = \frac{\$487}{1+i}^1$

$\text{PV(Outflows)} = \text{PV(Inflows)}$ ⇨ $\$358 = \frac{\$487}{1+i}^1$

$\$358 = \frac{\$487}{1+i}$ ← this is challenging because the i is in the denominator…

$1+i = \frac{487}{358} = 1.3603$ ← subtract 1 from both sides.

$1+i - 1 = 1.3603 - 1$

$i =.3603 = 36.03\%$

The IRR is $36.03\%$

✏️ Suppose I lend $358 today and am paid back $487 in 3 years. What is the effective interest rate on the loan?

✔ Click here to view answer

Write down formula from my perspective:

$\text{PV(Outflows)} = \$358$

$\text{PV(Inflows)} = \frac{\$487}{(1+i)^3}$

$\text{PV(Outflows)} = \text{PV(Inflows)}$ ⇨ $\$358 = \frac{\$487}{(1+i)^3}$

$(1+i)^3 = \frac{487}{358} = 1.3603$

$(1+i)^3 = 1.3603$ ← take $\frac{1}{3}$ power of both side (ie take the 3rd root of both sides)

$(1+i)^{(\frac{1}{3})} = (1.3603)^{\frac{1}{3}}$

$(1+i) = 1.3603^{\frac{1}{3}} = (1.3603)^{\frac{1}{3}} = 1.10801311092$

$1+i = 1.10801311092$

↑ you will use exactly these algebraic steps to solve the Yield to Maturity of a Zero Coupon Bond. Bruce will introduce you to all of these pieces of Jargon after the midterm (you don’t need them now), but because all rates of return are IRRs, you’ll use exactly the algebra above.

A shortcut if there are only two cash flows:

✏️ Suppose I borrow x today and pay back y in 1 year. What is the effective interest rate on the loan?

✔ Click here to view answer

In any IRR question, you write down $\text{PV Inflows} = \text{PV Outflows}$. Let’s do it from the perspective of the lender.

$x = \frac{y}{(1+i)^1}$ ← switcheroo

$1 + i = \frac{y}{x}$

$1 + i - 1 = \frac{y}{x} = 1$

$i = \frac{y}{x} - 1 = \frac{y - x}{x} = \frac{108 - 100}{100} = 8\% = \frac{\text{new} - \text{old}}{\text{old}}$

✏️ Suppose you are starting a business. The business will cost $600,000 to start up today. Starting in 1 year will pay you $80,000 every year, forever. Similar investments earn 5% per year.

1. If someone invested the $600,000 and created the business, then wanted to sell it to Kevin O’Leary, what would the fair value be?
2. What is the NPV of starting the business (ie what is the profit of starting the business)? What does the NPV rule advise?
3. What is the IRR of starting the business. What does the IRR rule advise?

✔ Click here to view answer

Whenever payments go on “forever” you will use the perpetuity formula:

Part 1.)
The fair value of the business is the PDV of the income you get from the business. We want the PV of the $80,000 every year, forever.

$PV = \frac{Pmt}{i} = \frac{\$80,000}{5\%}=\$1,600,000$ ← perpetuity formula

Extra [you’re not responsible for this!!]: If the cash flows grow at 2% per year, use the growing perpetuity formula:

$PV = \frac{Pmt}{i-g} = {\$80,000}{5\%-2\%} = \$2.67M$
Part 2.)

$\text{PV Inflows} = \frac{Pmt}{i} = \frac{\$80,000}{5\%}= \$1,600,000$

$\text{PV Outflows} = \frac{\$600,000}{(1+5\%)^0} = \$600,000$
$NPV = \text{PV (Inflows)} - \text{PV (Outflows)} = \frac{\$80,000}{5\%} - \$600,000 = \$1,000,000$

NPV rule 👍 Take it!

Part 3.)

for any IRR problem, solve it by writing down a formula [PV(Outflows) = PV(Inflows)] and then solving for i

$\text{PV (Outflows)} = \$600,000 = \text{PV (Inflows)} = \frac{\$80,000}{i}$ ← perpetuity formula, leaving i as a variable.

Recopy: $\$600,000 = \frac{\$80,000}{i}$

Switcheroo: $i = \frac{80,000}{600,000} = 13.33\%$

IRR calculations are simple for a perpetuity, so for a perpetuity bond, called a “consol” you can use this same simpler algebra.

The return on this investment is essentially 13.33%. Similar investments earn 5% per year. Therefore, this investment is very attractive. This is an example of the IRR rule. Because IRR=13.33% > opp cost of cap = 5%, undertake project.

✏️ Suppose you are paid in advance for a contract. You will be paid $20,000 today, but must provide services in 2 years that will cost $25,000. What is the IRR?

✔ Click here to view answer

$PVOut = PVIn$

Switch: $(1+i)^2 = \frac{25}{20}=1.25$ → Next, take square root of both sides.

$1+i = 1.25^{\frac{1}{2}} = .118$

$i = 0.118 = 11.8\%$

Side Note: the IRR rule assumes that you are in the role of an investor. An investor always wants a high return on their investment, so the IRR rule assumes that you should choose any project with a high IRR. (In particular, it says that you should choose any project with an IRR higher than your cost of capital/discount rate.) When you are paid in advance, the IRR is actually the rate of return that you are paying someone else. Naturally, if you are paying an interest rate to someone else, you would prefer a low interest rate rather than a high interest rate. Therefore, just as a sidenote, we don’t use the IRR rule when we receive the money upfront and have the costs later on. In cases like this, you are more like a borrower (who wants a low IRR) than a lender (who wants a high IRR). Basically, when you receive the money upfront, you want a low interest rate/IRR, just like you would with a loan.

⇨ What if the total cash inflows are equal to the total cash outflows?

✏️ Suppose you can invest $60,000 today and then in each of the following 4 years, you will receive back $15,000

t	[net] cf
0	-60,000
1	15,000
2	15,000
3	15,000
4	15,000

Notice that the cash inflows are equal to the cash outflows. IRR is like the interest rate on a bank deposit. If you deposit $60,000 and then you withdraw $60,000 and you can’t withdraw any more money (ie the account is empty), what must your interest rate be?

Clearly, you weren’t earning any interest, so i=0%. Let’s guess that the IRR=0% for this problem.

✔ Click here to view answer

I call this methodology GUESS AND CHECK.

$\text{PV (Outflows)} = 60,000$

$\text{PV (Inflows)} = \frac{15,000}{1+i}^1 + \frac{15,000}{(1+i)^2} + \frac{15,000}{(1+i)^3} + \frac{15,000}{(1+i)^4}$

The IRR is the i that solves the $\text{PV (Outflows)} = \text{PV (Inflows)}$:

$60,000 = \frac{15,000}{(1+i)^1} + \frac{15,000}{(1+i)^2} + \frac{15,000}{(1+i)^3} + \frac{15,000}{(1+i)^4}$

$60,000 = \frac{15,000}{(1+0\%)^1} + \frac{15,000}{(1+0\%)^2} + \frac{15,000}{(1+0\%)^3} + \frac{15,000}{(1+0\%)^4}$

$60,000 = \frac{15,000}{1^1} + \frac{15,000}{1^2} + \frac{15,000}{1^3} + \frac{15,000}{1^4}$

$60,000 = \frac{15,000}{1} + \frac{15,000}{1} + \frac{15,000}{1} + \frac{15,000}{1}$

$60,000 = \frac{15,000}{1} + \frac{15,000}{1} + \frac{15,000}{1} + \frac{15,000}{1}$

Note that $=0\%$ solves this equation. It’s the only number that does, so it is the IRR.

Intuitively, Notice that the cash inflows are equal to the cash outflows. IRR is like the interest rate on a bank deposit. If you deposit $60,000 and then you withdraw $60,000 and you can’t withdraw any more money (ie the account is empty), what must your interest rate be? Clearly, you weren’t earning any interest, so $i=0\%$. Let’s guess that the $IRR=0\%$ for this problem.

Keyboard speed tip:

✏️ Write down the formula for the present value of an annuity where you get $100 each year for the next 15 years. $i=5\%$

✔ Click here to view answer

$PV = \frac{\$100}{(1+5\%)^1} + \frac{\$100}{(1+5\%)^2} + \frac{\$100}{(1+5\%)^3} + \frac{\$100}{(1+5\%)^4} + \frac{\$100}{(1+5\%)^5}+ \frac{\$100}{(1+5\%)^6} + \frac{\$100}((1+5\%)^7) + \frac{\$100}{(1+5\%)^8} + \frac{\$100}{(1+5\%)^9} + \frac{\$100}{(1+5\%)^{10}} + \frac{\$100}{(1+5\%)^{11}} + \frac{\$100}{(1+5\%)^{12}} + \frac{\$100}{(1+5\%)^{13}} + \frac{\$100}{(1+5\%)^{14}} + \frac{\$100}{(1+5\%)^{15}}=\$1,037.97$

If someone wanted to give you a 15 year annuity, which would pay you $100 per year for 15 years, and wanted to sell you that for $1100, you wouldn’t take it because the fair value is $1,037.97.