👨‍🏫 Notes

Formulas for this lecture can be found in my paper formula sheets and online formula sheet.

Formulas for Reserves

The Fed decides how many dollars of reserves a bank is legally required to hold for every $\$100$ of deposits:

$$\begin{aligned} Dollars \;of \;Required \;Reserves &= R \times Checking \;Deposits \\ \$200M &= 10\% \times \$2B \end{aligned}$$

Explanation: banks are legally required to hold reserves to help lessen bank runs and banking panics (like with SVB and the regional banks).

Both Vault Cash and Deposits at the Fed are readily available cash, so both count as legal reserves:

$$Total \;Reserves = Vault \;Cash + Deposits \;at \;the \;Fed$$

Explanation: The Federal Reserve is the Central Bank of the USA. Deposits at the Fed may also be called “Deposits at the Central Bank.”

If a bank holds more reserves than it is legally required to hold, these are called “Excess Reserves:“

$$Excess \;Reserves = Total \;Reserves - Required \;Reserves$$

Formulas for Reserve Ratios:

$$Required \;Reserve \;Ratio = R = \frac{Dollars \;of \;Required \;Reserves}{Checking \;Deposits}$$ $$Excess \;Reserve \;Ratio = E = \frac{Dollars \;of \;Excess \;Reserves}{Checking \;Deposits}$$ $$Total \;Reserve \;Ratio = R+E = \frac{Dollars \;of \;Total \;Reserves}{Checking \;Deposits}$$

Note: if Bruce simply provides “deposits,” he is probably giving you “checking deposits.” He’s not terribly interested in the distinction between checking and savings deposits.

Bank profitability and leverage

Profitability and Interest:

$$\begin{aligned} Profit &= ΔContractPrice \times ContractSize \\ &= (\$4.70-\$4.50)\times 5000 \\ &=\$1000 \end{aligned}$$ $$\begin{aligned} Net \;Interest \;Spread &= (interest \;rate \;earned \;on \;assets) \\ & \quad - (interest \;rate \;paid \;on \;liabilities) \\ &= 7\% - 3\% = 4\% \end{aligned}$$ $$\begin{aligned} Net \;interest \;income &= (total \;interest \;received \;on \;assets) \\ & \quad − (total \;interest \;payments \;on \;liabilities) \\ &= \$700M - \$200M = \$500M \end{aligned}$$ $$\begin{aligned} Net \;interest \;margin &= \frac{Net \;interest \;income}{net \;interest \;earning \;assets} \\ &= \frac{\$500M}{\$10B} = 5\% \end{aligned}$$

Profitability Ratios:

Suppose Citizen’s bank has $\$200B$ of Assets, $\$180B$ of liabilities, $\$20B$ of Capital, and an annual profit after taxes of $\$2B$:

$$\begin{aligned} ROA &= \frac{Profit \;after \;taxes}{Assets} \\ &= \frac{\$2B}{\$200B} = 1\% \end{aligned}$$

Or, equivalently: $Proft \;after \;taxes = Assets \times ROA$

$$\begin{aligned} ROE &= \frac{Profit \;after \;taxes}{Capital} \\ &= \frac{\$2B}{\$20B} = 10\% \end{aligned}$$

Or, equivalently: $Proft \;after \;taxes = Capital \times ROE$

$$\begin{aligned} Leverage &= \frac{Assets}{Capital} \\ &= \frac{\$200B}{\$20B} = 10 \;to \;1 \end{aligned}$$ $$\begin{aligned} Debt \;To \;Equity &= \frac{Liabilities}{Capital} \\ &= \frac{\$180B}{\$20B} = 9 \;to \;1 \end{aligned}$$ $$ROE = ROA \times Leverage$$ $$Bank \;profit \;or \;loss = Change \;in \;Bank \;Capital$$

The Money Multiplier

The first green equation says that you multiply reserves by the money multiplier to get total deposits.

• You can also use the first equation with Open Market Operations
• A variation to calculate the total deposits in the economy:
• $Total \;Deposits \;in \;economy = Reserves \;in \;economy \times \frac{1}{R + E}$

The second green equation follows from the definition of M1

Example: Suppose I walk in off of the street and deposit $\$10,000$

⚡There are no balance sheet categories other than those listed:

Assets	Liabilities + BC
100M Vault Cash 600M Deposits at Fed 5B Auto Loans 10B Mortgages	? Checking Deposits 4B of Other Liabilities 1B Bank Capital

Suppose $R=0\%$. What is $E$?
$Assets=100+600+5000+10000= \$15.7B$
$Liabilities \;must \;be \;\$15.7B - \$1B = \$14.7B$
$\$10.7B \;of \;Checking \;deposits.$

Assets: 15.7B	Liabilities(14.7B) + BC(1B)
100M VC 600M DaF 5B Auto Loans 10B Mortgages	10.7B Deposits 4B of Other Liabilities 1B Bank Capital

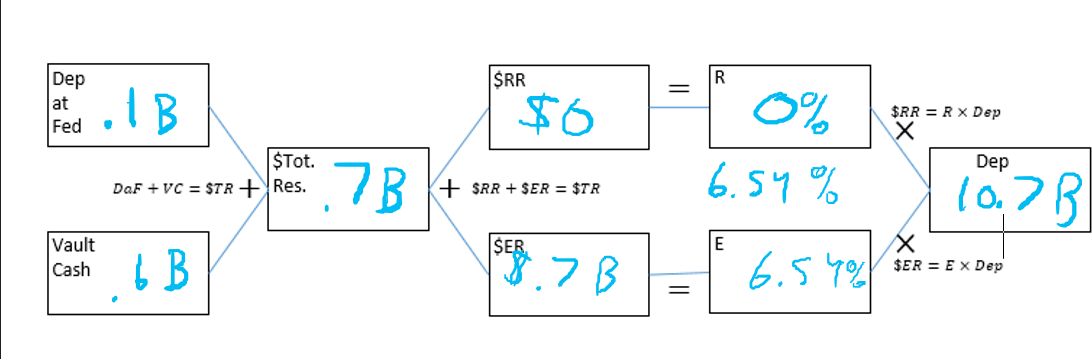
$$\begin{aligned} \$Reserves &= VC + DaF \\ &= \$100M + \$600M \\ &= \$700M \end{aligned}$$ $$\begin{aligned} R+E &= \frac{\$Total \;Reserves}{\$Checking \;Deposits} \\ R+E &= \frac{.7}{10.7}=0.0654 \\ R+E &= 6.54 \end{aligned}$$

$R=0\%$, so $E=6.54\%$

There are more questions like this here: ✏️ Balance Sheets Reserve Ratio Questions

⚡Revisit the above problem, assuming you don’t know R. What is the Money Multiplier? Hint: we know that $MM = \frac{1}{R+E}$, so we only need to find $R+E$ to calculate the $MM$.

✔ $Total \;Reserves = 700M$
$Deposits = 10,700M$
$R+E =\frac{\$Total Reserves}{Deposits} = 6.54\%$
$MM = \frac{1}{R+E} = \frac{1}{6.54\%} = 15.29$

⚡Suppose $R=10\%$ and $E=5\%$. Given the following balance sheet, what are the deposits at the Fed?

Assets	Liabilities
200M VC ? Deposits at the Fed 5B Auto Loans ? other assets	$10B Checking Deposits $4B Other Liabilities ? Bank Capital

✔ We can’t use $Assets=Liabilities+Bank\;Capital$, because there are too many ’?‘s on in the balance sheet. However, we know $R+E$ and Deposits, so we can figure out the number of reserves.

$R=10\%$ means that the government has required banks to hold $10\%$ of their deposits as reserves.

$$\begin{aligned} \$Required\;Reserves &= R \times Deposits \\ &= 10\% \times 10B \\ &= \$1B \;of \;required \;reserves. \end{aligned}$$

We also know that $E=5\%$. This means that the banks hold $5\%$ of their deposits as “extra reserves,” beyond the required reserve. The total dollar amount of excess reserves is:

$$\begin{aligned} \$Excess \;Reserves &= E \times Deposits \\ &= 5\% \times \$10B = \$.5B \end{aligned}$$

Here is another way to approach it:

$Total\;Reserves = (R+E) \times Deposits$
$R+E=15\%$
$R+E = \frac{Total\;Reserves}{Deposits}$

Therefore, this bank has $\$1B + \$.5B = \$1.5B$ of reserves. If it has $\$200M$ of Vault Cash, how many deposits at the Fed does it have?

$$\begin{aligned} Total \;Reserves &= Vault \;Cash \\ & \quad + Deposits \;at \;Fed \end{aligned}$$

(Interpretation: Both Vault Cash and cash deposited at the Fed count as legal reserves.)

$$\begin{aligned} \$1.5B &= \$200M \\ & \quad + Deposits \;at \;the \;Fed \end{aligned}$$

$Deposits \;at \;Fed = \$1.3B$
$Total Reserves = (R+E) \times Deposits$