Skip to content
Rob's e2000 Notes

✏️ Final Exam Practice

Tip: Working through these problems with a formula sheet handy is a great way to learn and get comfortable with the formula sheet. This will help you use the formula sheet quickly and confidently during the exam.

You can download my paper formula sheets at https://robmunger.com/2000share. If this is your first time using them, the “Basic” (not “Text”) sheet has all of the formulas and may be slightly more readable. There is also an online version on this website.

Bond

✏️ What is the price of the following bond?
F = $5000
c = 12%
i = 13%
T = 4

✔ Click here to view answer

Key equations from the formula sheet:

PB=Fc(1+i)1+Fc(1+i)2+⋯+Fc(1+i)T+F(1+i)TP_B = \frac{Fc}{(1 + i)^1} + \frac{Fc}{(1 + i) ^ 2} + ⋯ + \frac{Fc}{(1 + i)^T} + \frac{F}{(1 + i)^T}

The coupon payment is Fc=12%×$5000=$600Fc=12\%×\$5000=\$600

PB=$600(1+13%)1+$600(1+13%)2+$600(1+13%)3+$600(1+13%)4+$5000(1+13%)4=$4851.28P_B = \frac{\$600}{(1+13\%)^1} + \frac{\$600}{(1+13\%)^2} + \frac{\$600}{(1+13\%)^3} + \frac{\$600}{(1+13\%)^4} + \frac{\$5000}{(1+13\%)^4} = \$4851.28

Here’s a shorter way to calculate it:

PB=$6001.131+$6001.132+$6001.133+$56001.134=$4851.28P_B = \frac{\$600}{1.13^1} + \frac{\$600}{1.13^2} + \frac{\$600}{1.13^3} + \frac{\$5600}{1.13^4} = \$4851.28

✏️ What is the price of the following bond?
F = $5000
c = 0
i = 13%
T = 10

✔ Click here to view answer

Key equations from the formula sheet:

PZCB=F(1+i)TP_{ZCB} = \frac{F}{(1+i)^T}
PZCB=$5000(1+13%)10=$1472.94P_{ZCB} = \frac{\$5000}{(1+13\%)^{10}} = \$1472.94

✏️ What is the price of the following bond?
F = $5000
c = 12%
i = 13%
T = ∞

✔ Click here to view answer

Key equations from the formula sheet:

PConsol=FciP_{Consol} = \frac{Fc}{i}
PConsol=(12%×$5000)13%=$4615.38P_{Consol} = \frac{(12\%×\$5000)}{13\%} = \$4615.38

✏️ What is the YTM of the following bond?
F = $5000
c = 12%
T = ∞
PB = $8000

✔ Click here to view answer

Key equations from the formula sheet:

PConsol=FciP_{Consol} = \frac{Fc}{i}

To answer a YTM problem, you write down the bond pricing formula and solve it for i.

$8000=$5000×12%i\$8000 = \frac{\$5000×12\%}{i}

Algebra (Switcheroo):

i=$5000×12%$8000=7.5%i = \frac{\$5000×12\%}{\$8000} = 7.5\%

The following would be a stretch question. I wouldn’t expect a question this hard on the exam.

✏️ What is the price of the following bond?
F = $5000
c = 0
T = 10
PB = $3000

✔ Click here to view answer

Key equations from the formula sheet:

PZCB=F(1+i)TP_{ZCB} = \frac{F}{(1+i)^T}

For any YTM problem, you write down the bond pricing formula and solve for i.

$3000=$5000(1+i)10\$3000 = \frac{\$5000}{(1+i)^{10}}

Algebra/Switcheroo:

(1+i)10=$5000$3000=1.6667(1+i)^{10} = \frac{\$5000}{\$3000} = 1.6667

Recopy:

(1+i)10=1.6667(1+i)^{10} = 1.6667

Take the 1/10 power of both sides:

(1+i)=1.6667110(1+i) = 1.6667^{\frac{1}{10}}

You can enter this into most spreadsheets as 1.6667^(1/10) or 1.6667^.100. For many calculators, you would replace the caret, ^, with a dedicated button, such as a yxy^x or xyx^y button. Whether you use a calculator or spreadsheet, be careful with exponents that aren’t round numbers, though. Don’t forget the parentheses around (1/10)!

(1+i)=1.0524(1+i) = 1.0524

Subtract 1 from both sides:

i=1.0524−1=5.24%i = 1.0524-1 = 5.24\%

We can check our math by substituting 5.241% back into the bond pricing equation and confirming that we get a price close to our original bond price of 3000.Inthiscase,I′vedonethecalculationswithhighprecisiontoensurethattheanswercomesoutverycloseto3000. In this case, I've done the calculations with high precision to ensure that the answer comes out very close to 3000.

PZCB=$5000(1+5.24%)10=$3000.28P_{ZCB} = \frac{\$5000}{(1+5.24\%)^{10}} = \$3000.28

CAPM

✏️ Suppose that for a given firm, β=1.3. The expected return on the market is 13%, and the risk free rate is 5%. What is the Expected return for this stock?

✔ Click here to view answer

Key equations from the formula sheet:

E(rS)=rF+β[E(rM)−rF]E(r_S) = r_F + β[E(r_M) - r_F]E(rS)=5%+1.3[13%−5%]=15.4%E(r_S) = 5\% + 1.3[13\% - 5\%] = 15.4\%

✏️ Suppose that for a given firm, β=1.3. The Market Risk Premium 10%, and the risk free rate is 5%. What is the Expected return for this stock?

✔ Click here to view answer

Key equations from the formula sheet:

E(rS)=rF+β[E(rM)−rF]E(r_S) = r_F + β[E(r_M) - r_F]

“Risk Premium” means you subtract off the risk free rate.
E(rM)−rF=E(r_M) - r_F = Market risk premium = Expected risk premium of market

We have been given the market risk premium, so E(rM)−rF=10%E(r_M) - r_F = 10\%
If rF=5/r_F = 5/%, then E(rM)−5%=10/E(r_M) - 5\% = 10/%, so E(rM)=15/E(r_M) = 15/%.
Now, we can apply the formula:

E(rS)=rF+β[E(rM)−rF]=5%+1.3×(15%−5%)=18%E(r_S) = r_F + β[E(r_M) - r_F] \\ \qquad = 5\% + 1.3×(15\%-5\%) = 18\%

EMH Stock Price

✏️ You are considering purchasing a share of XYZ Corp. There is a 30% chance that in one year, the stock price will be $110, a 40% that it will be $120, and a 30% that it will be $130. You expect to receive a $1 dividend in one year. Given the riskiness of XYZ corp, similar corporations are earning a return of 14%. What is the fair price of XYZ stock right now?

✔ Click here to view answer EV=30%×$110+40%×$120+30%×$130=$120EV = 30\% × \$110 + 40\% × \$120 + 30\% × \$130 = \$120Price = PDV of EV + PDV of dividend\text{Price }=\text{ PDV of EV }+\text{ PDV of dividend}Price =1201.14+11.14=$106.14\text{Price }= \frac{120}{1.14} + \frac{1}{1.14} = \$106.14

Options

✏️ Draw a short call with a strike price of $45 and a premium of $2

✔ Click here to view answer

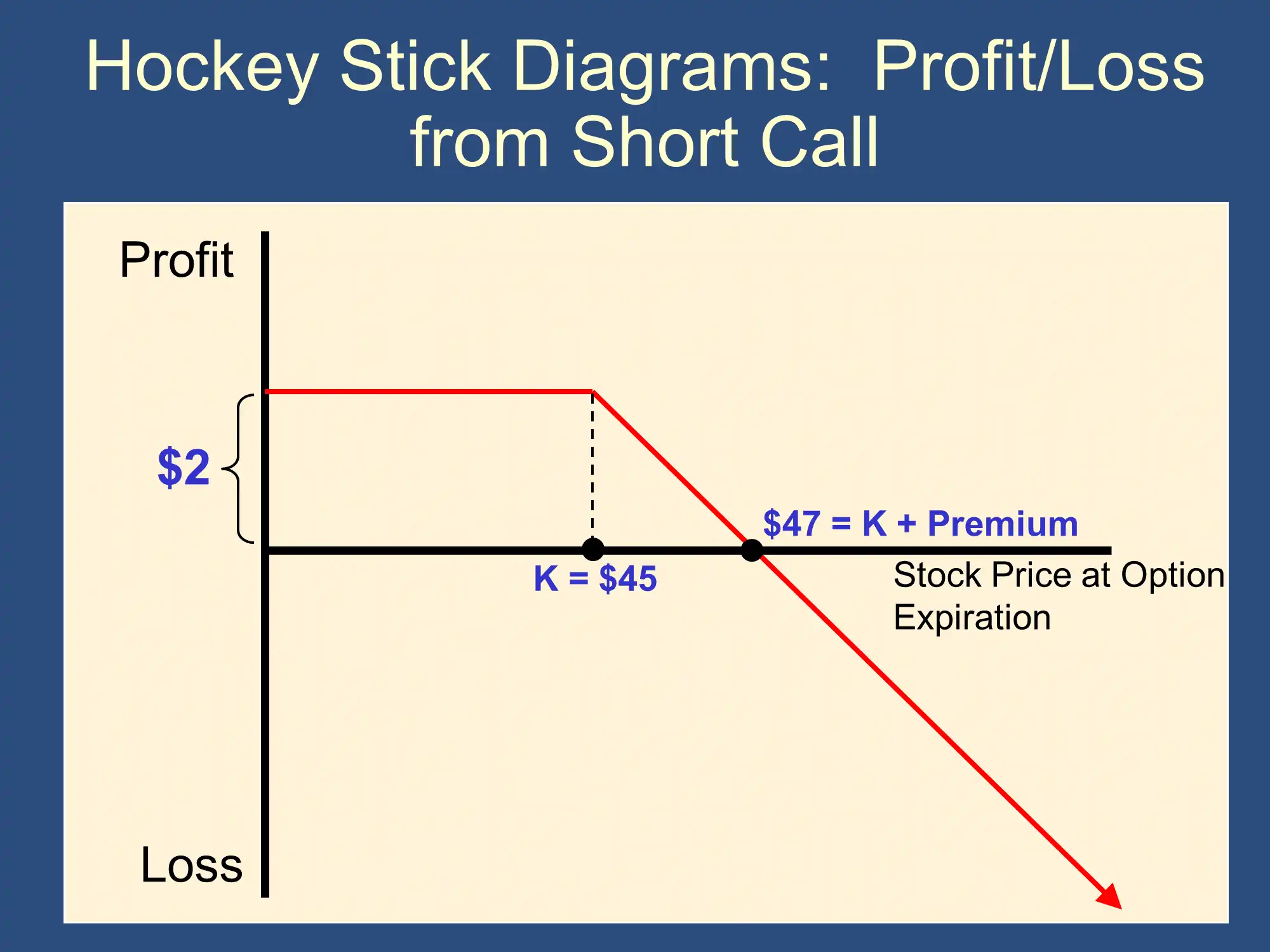
✏️ What is your P/L on the above short call if S=$38 at expiration? If it equals $52 at expiration? Also, what are your total profits or losses per contract?

✔ Click here to view answer

Key equation from the formula sheet:

P/L from Selling a Call = Pr - Max (S-K, 0)
When S=$38:
P/L from Selling a Call = Pr - Max (S-K, 0) = $2 - $0 = $2 per share
When S=$52:
P/L from Selling a Call = Pr - Max (S-K, 0) = $2 - Max($52-$45,0) = $2 - $7 = -$5 per share

Your total profits or losses from a full contract are $200 and -$500, respectively.

✏️ Suppose S=$43 on the above option and premium is $2. What is the IV and TV?

✔ Click here to view answer

Key equations from the formula sheet:

Call IV = Max (S-K, 0)
Premium = Intrinsic Value + Time Value

Call IV = Max (S-K, 0) = Max($43-$45, $0) = $0

Premium = Intrinsic Value + Time Value
$2 = $0 + Time Value, so the time value is $2.

✏️ Suppose that S=$42 on the above K=$45 option and the time value of the option is $3. What is the premium?

✔ Click here to view answer

Call IV = Max (S-K, 0) = Max ($42-$45, 0) = Max (-$3, $0) = $0
Premium = Intrinsic Value + Time Value = $0 +$3 = $3

Option Strategies

✏️ Consider a bull spread with the following options.

A K=$35 call has a premium of $4
A K=$40 call has a premium of $1

Construct a bull spread from these options.

✔ Click here to view answer

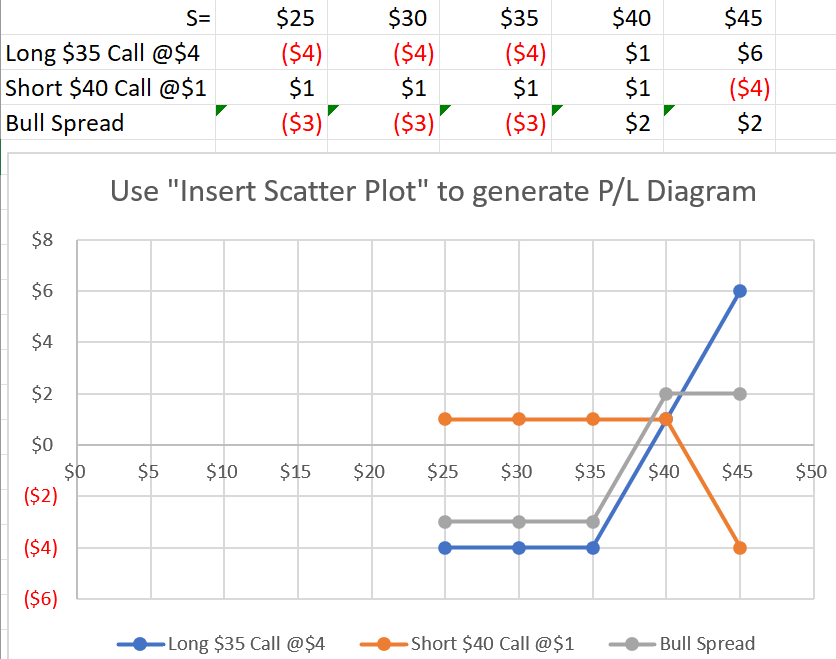
Buy the $35 Call and Sell the $40 Call.

✏️ Suppose you Buy the $35 Call and Sell the $40 Call. This allows you to construct a bull spread. The $35 Call has a premium of $4 and the $40 call has a premium of $1. Suppose S=$33.
What is your P/L of the Call you purchased? Show your work.

✔ Click here to view answer

You purchased a $35 Call for $4. Because S=$33, you will not exercise this call. It will expire worthless. However, you will have paid $4 for the call, so your P/L is -$4.

✏️ What is your P/L of the Call you sold? Show your work.

✔ Click here to view answer

You sold a $40 call and received a premium of $1. Because S=$33, your counterparty will not exercise the call. You get to keep the premium of $1, so your P/L is $1. (If your counterparty exercised the call, they would be purchasing a stock worth only $33, but they would pay $40. They don’t want to do this!)

✏️ What is your P/L of the combined bull spread?

✔ Click here to view answer

For the call we purchased, P/L is -$4.
For the call we sold, P/L is $1
Combining them, -$4 + $1 = -$3

Extra Practice

(I call this extra practice because it goes beyond the level of difficulty I would anticipate on the exam. If you can do it, you are in great shape!)

✏️ Graph the bull spread in the previous examples, above.

✔ Click here to view answer
Microsoft Excel Workbook
Final Practice - Spreadsheet

Futures

✏️ Suppose that you are bullish on wheat and are sure that the price of wheat will rise in the coming weeks. Would you purchase or sell a wheat futures contract?

✔ Click here to view answer

Buying a futures contract is a bet that the futures price will rise, so you would buy the futures contract.

✏️ Suppose that you purchase the contract at 632 and that by the time the contract expires, the price has fallen to 629. The contract size is 3000 bushels. What is your total profit or loss?

✔ Click here to view answer

ΔContractPrice = (NewContractPrice - OldContractPrice)
ΔContractPrice = 620-632 = -3
Buy the contract:
P/L = ΔContractPrice * ContractSize
P/L = -3∗3000=−3 * 3000 = -9,000

✏️ Continuing the above problem, suppose that you deposited 10,000inyourmarginaccounttoopenthetrade.Howmuchwillremaininyourmarginaccountafterward?Supposetheinitialmarginis10,000 in your margin account to open the trade. How much will remain in your margin account afterward? Suppose the initial margin is 10,000 and the maintenance margin is $5,000 Will you get a margin call? If so, how much must you deposit?

✔ Click here to view answer

Initially, there was 10,000inyourmarginaccount.Youlost10,000 in your margin account. You lost 9,000, so there is only 1,000inyourmarginaccount.Because1,000 in your margin account. Because 1,000 < 5,000,youwillgetamargincallandwillneedtodepositadditionalmoney.Youneedtorefillthecoffeecupuntilthebalanceisequaltotheinitialmarginof5,000, you will get a margin call and will need to deposit additional money. You need to refill the coffee cup until the balance is equal to the initial margin of 10,000. To refill the cup from 1,000to1,000 to 10,000 will take a $9,000 deposit.